Insertion

Insertion in AVL tree is starts out similar to regular binary search trees. That is we do the following:

• Find the appropriate empty subtree where new value should go by comparing with values in the tree.
• Create a new node at that empty subtree.
• New node is a leaf and thus will have a height balance of 0
• go back to the parent and adjust the height balance.
• If the height balance of a node is ever more than 1 or less than -1, the subtree at that node will have to go through a rotation in order to fix the height balance. The process continues until we are back to the root.
• NOTE: The adjustment must happen from the bottom up

Example

Suppose we have start with the following tree (value on top is the value, value on bottom is the height balance

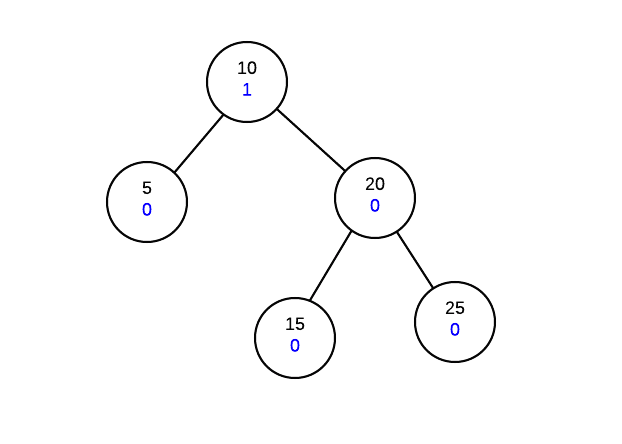
Insert 30

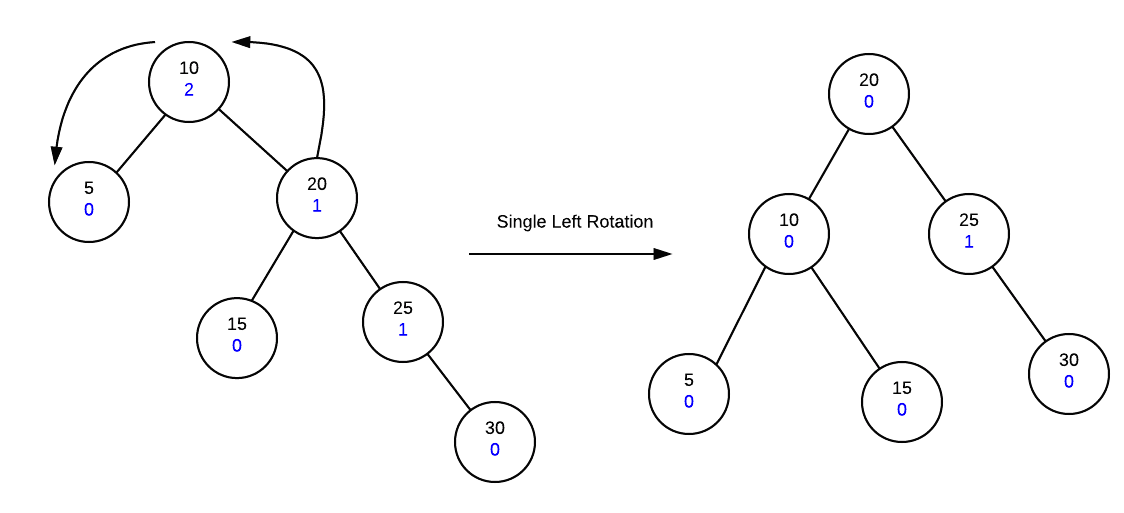
At this point, we have adjusted all the height balances along the insertion path and we note that the root node has a height balance of 2 which means the tree is not height balanced at the root.

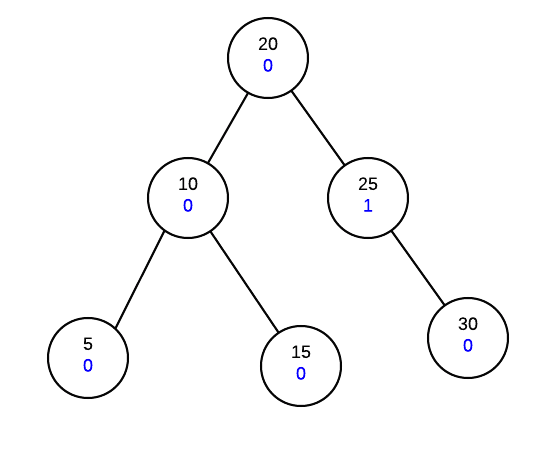
In order to fix our tree, we will need to perform a rotation

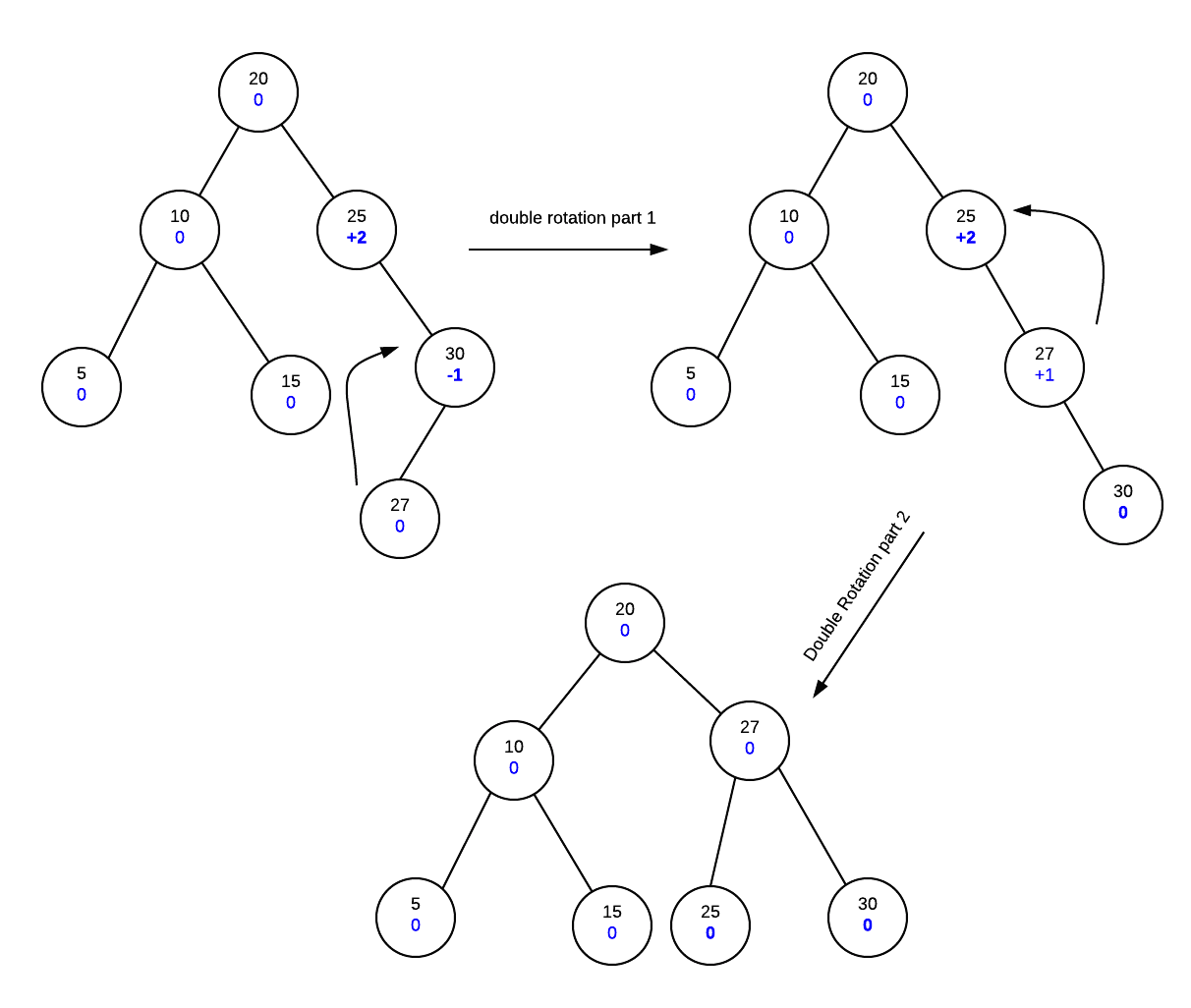
Insert 27

We start with our tree:

Now we find the correct place in the tree and insert the new node and fix the height balances

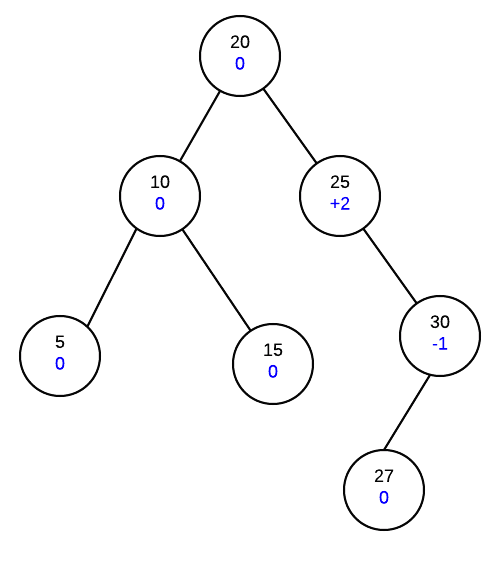
Now, as we reach node 25 and see that it the height balance is +2. If we then look at it's child's height balance we find that it is -1. As the signs are different, it indicates that we need a double rotation. Different signs indicate that the unbalance is in different directions so we need to do a rotation to make it the same direction then another to fix the unbalance.