Insertion Example
Starting with an empty tree let us take a look at how red-black tree insertions work.
In the pictures below, null nodes (empty subtrees) are denoted as black circles

Insert 30
All nodes are inserted as red nodes:
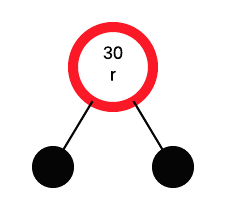
If the root is red, make it black:
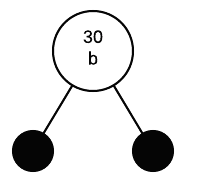
Insert 50
Insert 50 as a red node, parent is black so we don't have to change anything
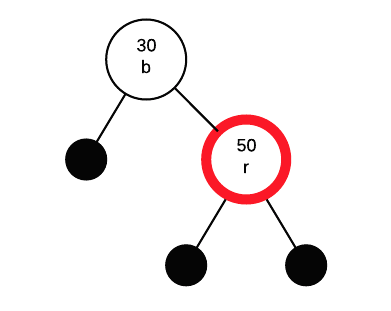
Insert 40
Inserting 40 as a red node.
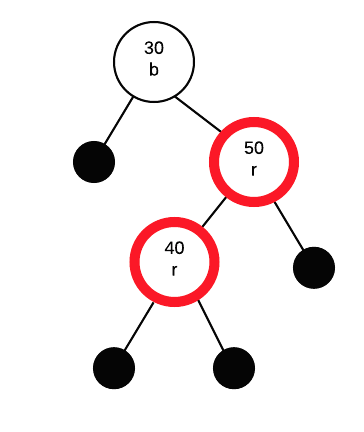
If parent is red, we must apply fix. Parent's sibling (50's sibling) is black, so we must perform a rotation.
The type of rotation depends on the insertion pathway. If the insertion path from grand parent to parent to node is straight (both left or both right) do a single rotation. If it is angled (left then right or right then left) we need to do a double.
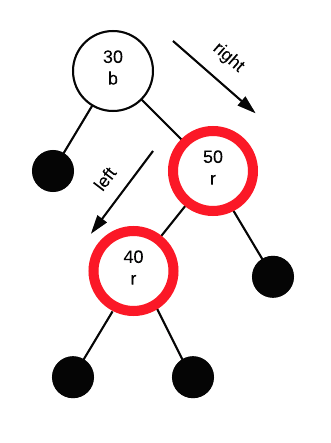
In this case, we need to do a double (aka zig zag) rotation.
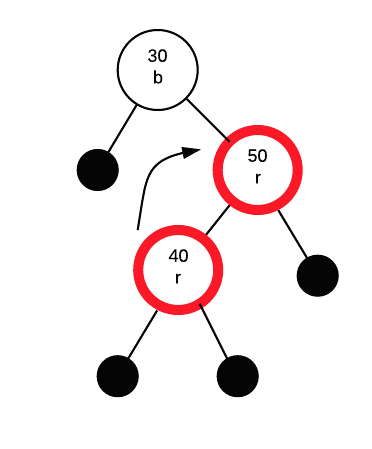
Rotate first 40 and 50
then rotate again with 30 and 40, this time doing a colour swap. A zigzag rotation is just an extra step that is needed to make the insertion path go in the same direction.
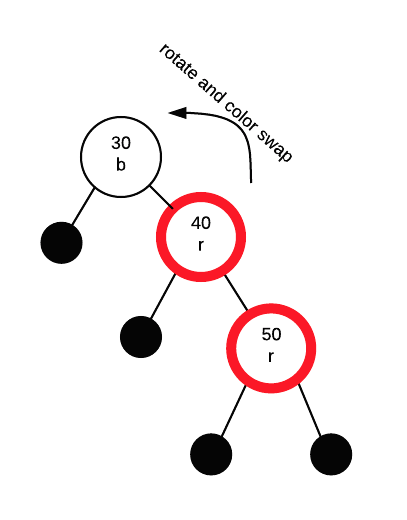
Finally we end up with:
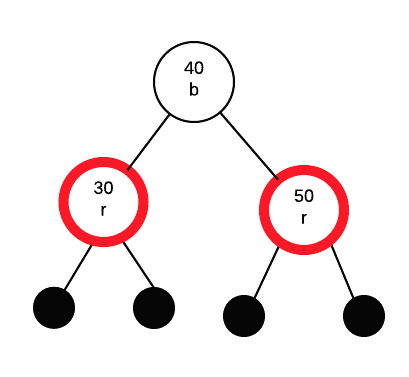
Insert 20
inserting 20 as a red node.
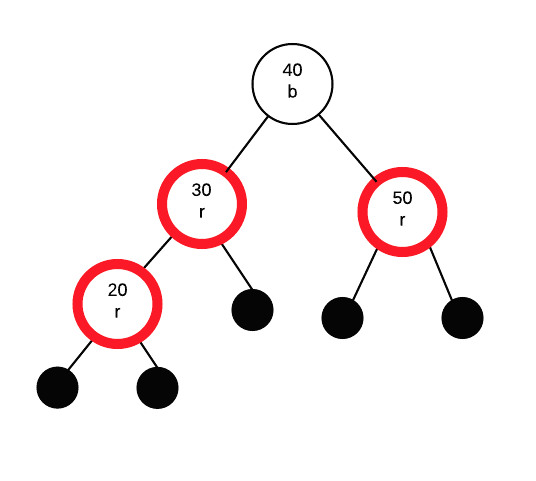
If parent is red we must apply a fix. Parent's sibling is red so we need to do a colour swap between parent+sibling and grandparent.
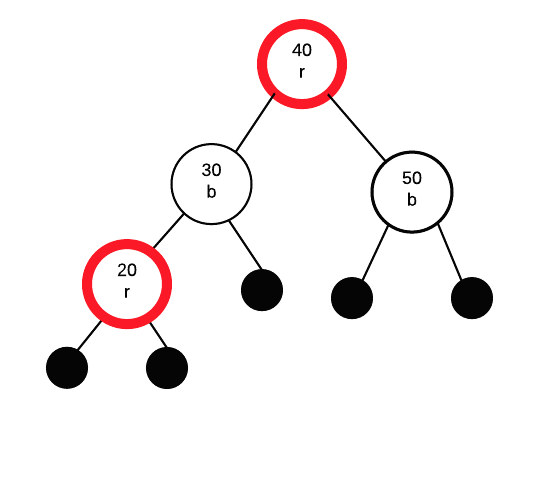
Now as 40 is the root of the whole tree we must change 40's colour to black. As it is the root, we can just change it to black without causing other problems.
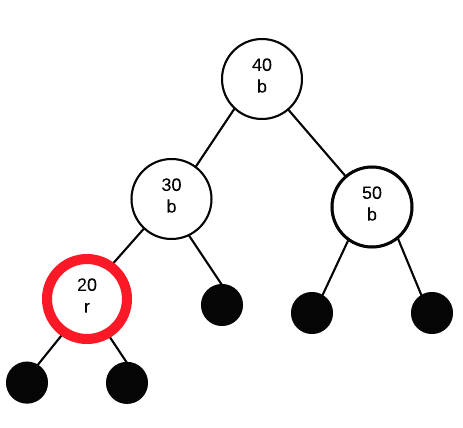
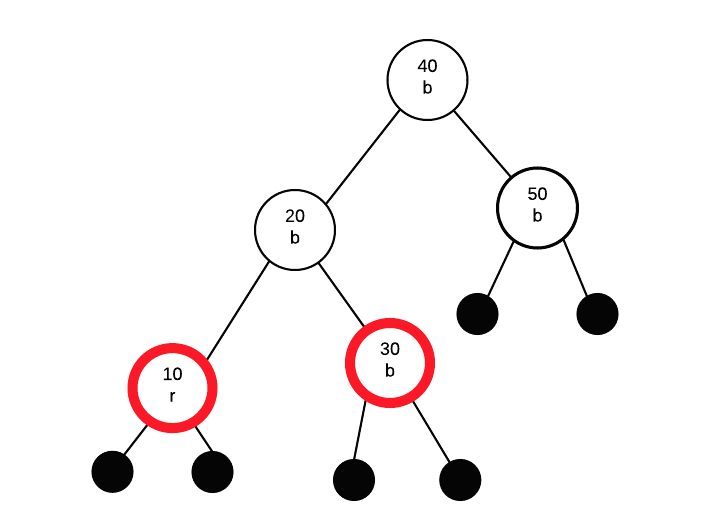
Insert 10
inserting 10 as a red node.
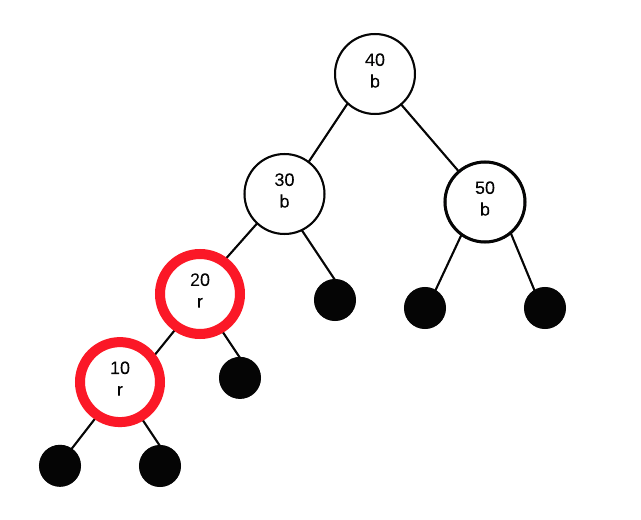
If parent is red, we must apply a fix. Parent's sibling is black, so a rotation is needed. This time, the insertion path from grandparent to parent to node is "left" then "left". Thus, we only need to perform a single rotation and colour swap.
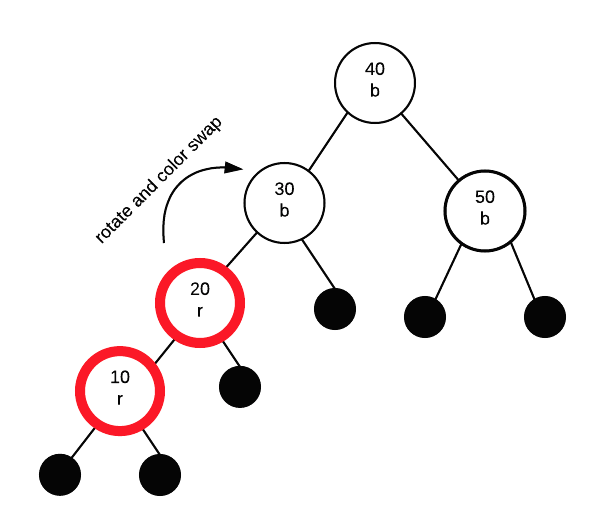
Finally we get: