Implementation of a heap

Clearly we want to implement the heap in as simple a manner as possible. Although we can use a link structure to represent each node and their children, this structure is actually not that good for a heap. One reason is that each node needs two extra pointers so for small data the memory needed for the pointers could easily exceed that of the data. Also, we really don't need the linking structure because our tree is a complete binary tree. This makes it very easy for us to use an array to represent our tree.

Idea is this. Store the data in successive array elements. Use the index values to find the child and parent of any node.

Suppose data was stored in element i. The left child of that node is in element 2i+1 The right child of the node is in element 2i+2 The parent of the node is stored in (i-1)/2 (for all but root node which has no parent)

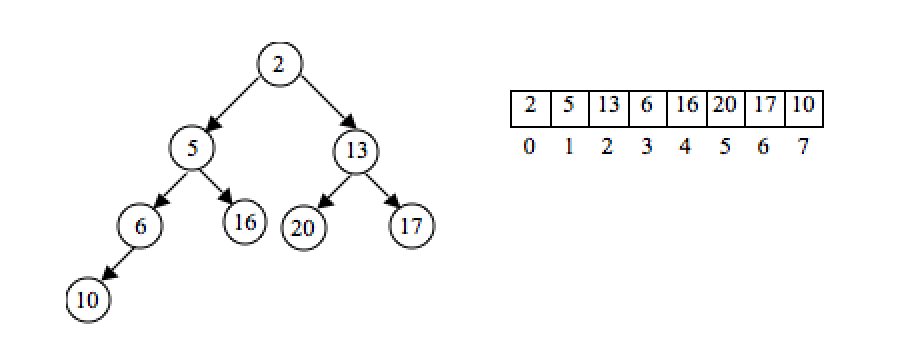
consider node with 5 in it. 5 is at element with index 1 in array. According to formulas:

Left child should be in index 2i+1 = 2(1)+1= 3 Right child should be in index 2i+2 = 2(1)+2 = 4 Parent is in index (i-1)/2 = (2-1)/2 = 1/2 = 0

This representation is very convenient because when we add values to the end of the array it is like we are adding a node to the leftmost available spot at the bottom level.

As long as we keep track of number of elements in the array, we do not have to worry about empty nodes.

We also eliminate any need for pointers or the overhead of allocating nodes as we go.