Example: the Factorial Function

Write the function:

int factorial(int n);

This function returns n! (read n factorial) where n is an integer.

n!=n* n-1* n-2*....2*1  by definition 0! is 1

for example

if n==5, then n! would be 5! = 5*4*3*2*1=120

To write this we must come up with several things. What is the base case? In other words, for what value of n do I immediately know what the answer would be without doing more than a simple operation or two.

In this case, we know what 0! is. It is 1 by definition 1! is another base case because 1! is simply 1 as well. However, it is not actually necessary to explicitly state the base case for when n is 1 as we can further reduce that to the 0! base case

So the base case occurs when n is 0 or 1. In this case, the function can simply return 1

Now the recursive case. How can we state the solution in terms of itself. First thing you should notice is that:

5!=5 * 4 * 3 * 2 * 1 but 4*3*2*1 is really 4!
So:

5! = 5* 4!  but 4! is just 4* 3!  and so on.

Thus if I had a function that can give me the factorial of any number I can use it to find the factorial of that number-1 and thus allowing me to calculate the factorial of the original by multiplying that result with number. In other words I can use the int factorial(int) function to solve int factorial(int)

int factorial(int n){
    int rc;              //stores result of function
    if(n==1 || n==0){    //check for base case
        rc=1;            //if n is 1 or 0 rc is 1
    }
    else{                //else it is recursive case
        rc=n * factorial(n-1);  //rc is n * (n-1)!
    }
    return rc;
}

Why does this work?

To understand why recursion works, we need to look at the behavior of the run time stack as we make the function calls:

Suppose we have the following program:

int fact(int n){
    int rc;              //stores result of function
    if(n==1 || n==0){    //check for base case
        rc=1;            //if n is 1 or 0 rc is 1
    }
    else{                //else it is recursive case
        rc=n * fact(n-1);  //rc is n * (n-1)!
    }
    return rc;
}
int main(void){
   int aa = fact(4);
}

When the program starts this is our run time stack:

fact(4) means that we call function fact() with 4 as argument so push that information onto the stack

Since we make a function call to fact(3) we must now push that information onto the stack also. Note, return statement not reached before calling fact(3) so stack isn't popped at this point

Again, because we are calling the function with fact(2) , we must also push this onto the stack

Once again, because we are calling the function with fact(1) we must also push this onto the stack

If we follow the code at this point we can see that we are able to reach the return statement without further function calls. Thus, we can now pop the stack.

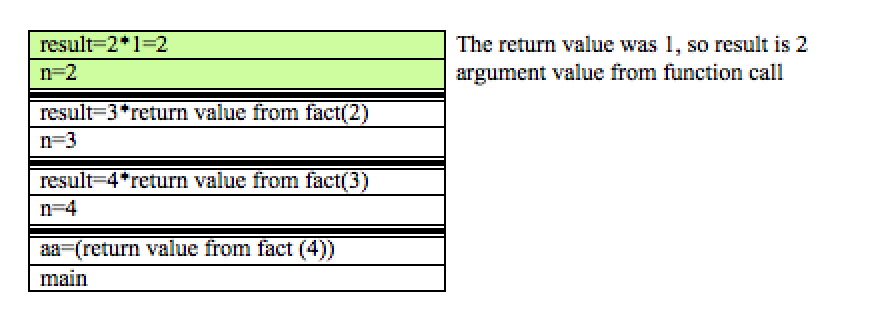
This will lead to the completion of the topmost function call and again, it can be removed from the stack. This time, the return value is used to solve the problem one more layer above:

This will lead to the completion of the topmost function call and again, it can be removed from the stack. This time, the return value is used to solve the problem one more layer above:

Finally, we can go back to main, as we have reached the final result: